The Science of Permeability

The study of permeability got a big jumpstart by a guy named Henry Darcy in the early 1800’s. Darcy was a French Engineer who started studying porosity and permeability while working on a municipal water transport system.
Henry Darcy, born in 1803, was tasked with designing a system that could transport water to the city of Dijon from a nearby spring. Before being transported, the water needed to be filtered through sand to remove sediments and impurities.
Darcy imagined that forcing the water through a sand filter would slow down its flow. He assumed friction and surface tension between the water and the walls of the pores would use up some of the water’s energy.
In order to ensure a proper flow rate, he needed to know exactly how much the water would be slowed down by the filters.
To find out, he designed an experiment.
Darcy’s Famous Experiment
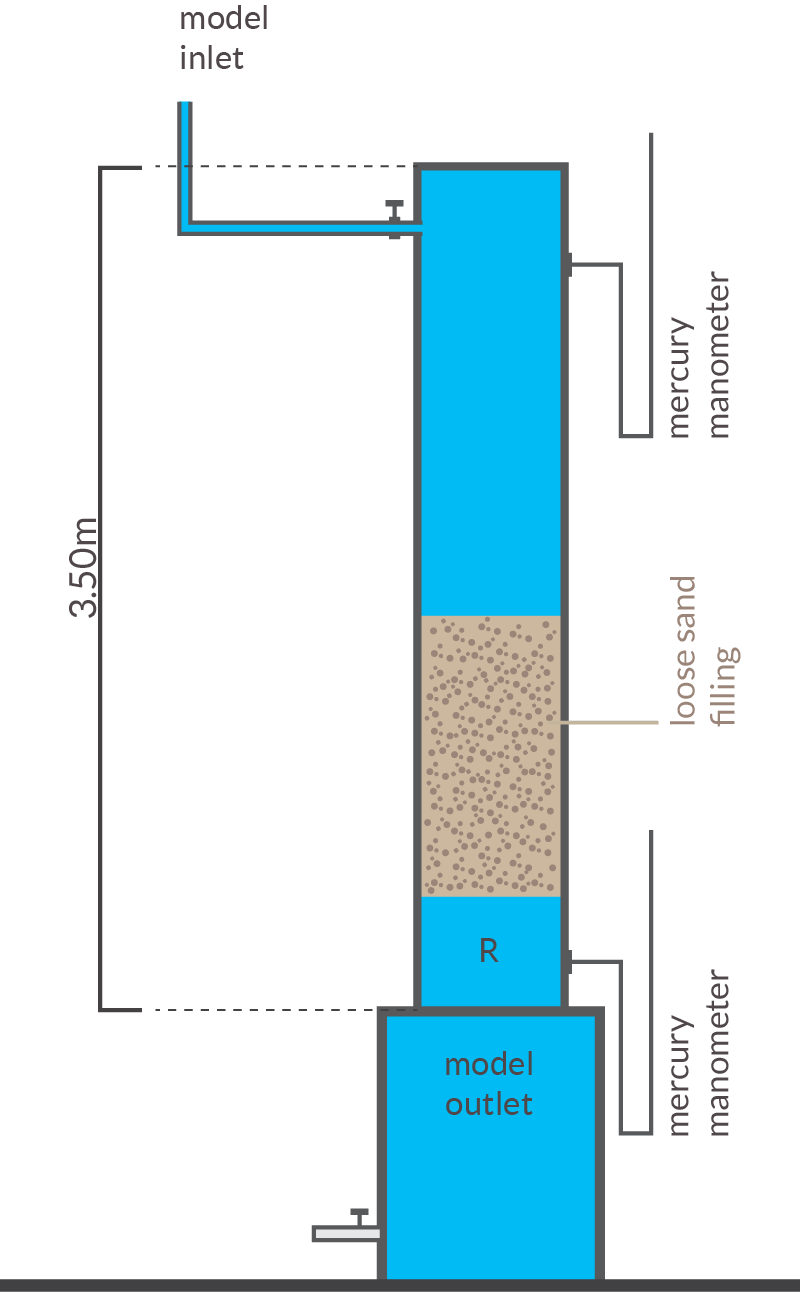
Working in the courtyard of a French hospital, Darcy build a hollow metal cylinder and filled it with a carefully measured amount of sand. He then hooked the hospital’s water supply, which maintained a relatively constant pressure, to the top of the cylinder.
Darcy measured the pressure at the top and bottom of the column in order to determine the pressure gradient, which is defined as the change in pressure divided by the distance over which that change occurs. He had a hunch that the higher the pressure gradient, the faster water would flow from the bottom of the cylinder. He reasoned that the energy contained in the water was potential energy related to the difference in pressure between the top and bottom of the filter. The more energy the water had to begin with, he figured, the more would be left over after passing through the filter and losing some energy to friction, assuming the filter was always the same.
In order to test his hunch, he varied the pressure gradient to measure its effect on the flow rate. Since the input pressure from the hospital water line was constant, and the pressure at the bottom of the column, where water poured out, was essentially 0, Darcy couldn’t easily adjust the pressure gradient by changing the pressure itself. Instead, Darcy changed the distance over which the change in pressure occurred by adding and removing sand (remember, hydraulic gradient is the change in pressure divided by the distance over which that change occurs).
In the end, Darcy’s hunch was correct: the rate that water passed through the sand filter was directly proportional to the pressure gradient.
Darcy’s experimental setup
After making many measurements using different sand column heights, sand types, and pressure differences, Darcy was able to develop an equation that would allow him to predict flow rates based on the pressure gradient, the porosity of the sand, and the viscosity of the water. This equation is now known as Darcy’s Law.
Darcy’s Law
Before we get into the math, it’s important to gain an intuitive understanding of Darcy’s Law.
Darcy’s law states that:
- The rate at which a liquid can flow through a permeable material is proportional to the permeability.
- The rate at which a liquid can flow through a permeable material is proportional to the pressure gradient.
- The rate at which a liquid can flow through a permeable material is inversely proportional to the viscosity of the liquid.
These three conclusions are all seemingly common-sensical. The real question is what are the proportions? What is the math?
Let’s break these statements down a bit.
The rate at which a liquid can flow through a permeable material is proportional to the pressure gradient:
The pressure gradient is the change in pressure divided by the distance over which the change occurs. The higher the pressure gradient, the faster liquids will flow.
The rate at which a liquid can flow through a permeable material is proportional to the permeability:
Permeability describes the degree to which the pore spaces in the material are connected. A sponge or a pile of gravel has a higher permeability than a shale, which has pores that are more poorly interconnected. Liquids flow faster through a material with a high permeability.
The rate at which a liquid can flow through a permeable material is inversely proportional to the viscosity:
The resistance of a liquid to flow, known as viscosity, is a value that is different for each type of fluid. For example, oil has a higher viscosity than water – it doesn’t flow as easily because it is thicker, even though it is lighter and slipperier. As the viscosity increases, the flow rate goes down as the result of the greater losses of energy to friction that occurs in viscous materials as they flow.
Darcy set about to answer the math questions. All he had to do was change the variables and observe the results.
In Darcy’s experiment, as the pressure of the water coming into the column was increased, the flow rate out of the filter increased. In some trials, Darcy shut off the water and allowed the column to drain. As the amount of water left in the column decreased, the pressure it exerted at the bottom of the column decreased, causing the flow rate to decline as the top of the water column dropped.
Darcy’s Law Equation
In its simplest form, Darcy’s law is written like this:
$$ R = \frac {k}{μ}\times \text{Pressure Gradient} $$
Each letter represents a variable that can be measured.
Let’s take a look at the variables.
R
R is the Rate at which water moves through the sand.
k
k represents the Permeability of the material that the liquid is flowing through. In the oil industry, it is still measured in “Darcys” in honor of Henry and can be determined by analyzing samples of the material in question.
μ
μ is the Viscosity of the liquid. The higher the viscosity, the more difficult it is for the liquid to flow (molasses has high viscosity). This can be measured in the lab.
Pressure Gradient
This is the change in pressure over the distance under consideration. In Darcy’s experiment, the pressure at the top of the column was set by the pressure of the hospital water supply. The pressure at the bottom of the column is essentially zero, assuming that the water drips out of the sand filter after it passes through. In order to change the pressure gradient, Darcy changed the distance over which the pressure went from the water supply pressure to zero by adding or removing sand from the filter.
In summary, Darcy’s Law tells us the following:
The higher the permeability, the faster liquids flow. The higher the pressure gradient, the faster liquids will flow. The higher the viscosity, the more slowly liquids flow. By plugging all the variables into the equation, we can calculate the flow rate.
How do we use Darcy’s Law now?
Darcy’s law doesn’t just work with sand filters and water. It works with any permeable material and and fluid, so it is useful in the oil and gas extraction industries. Among other things, Darcy’s Law can be used to:
- Determine how quickly oil will flow into a well
- Figure out how quickly production will decrease with time
- Calculate how reinjection of fluids will affect production
- Trace contaminants that enter the groundwater system underground or on the surface
Storing and Transporting Liquids Underground
Water, oil, and natural gas are stored underground in pores, tiny spaces between the individual grains of material making up the rocks. These spaces often form at the same time as the rock itself, although under certain conditions pore spaces can also form after deposition. Although each pore is very small, when added together, pores can make up a significant percentage of the volume of a rock. This percentage can be measured and is referred to as the porosity.
In general, porosity can range from 0% to 50%, depending on the rock type and its geologic history. The table below shows typical porosity ranges for common rocks and sediments.
| Soil Type | Porosity, pt |
|---|---|
| Unconsolidated deposits | |
| Gravel | 0.25 - 0.40 |
| Sand | 0.25 - 0.50 |
| Silt | 0.35 - 0.50 |
| Clay | 0.40 - 0.70 |
| Rocks | |
| Fractured basalt | 0.05 - 0.50 |
| Karst limestone | 0.05 - 0.50 |
| Sandstone | 0.05 - 0.30 |
| Limestone, dolomite | 0.00 - 0.20 |
| Shale | 0.00 - 0.10 |
| Fractured crystalline rock | 0.00 - 0.10 |
| Dense crystalline rock | 0.00 - 0.05 |
| Source: Freeze and Cherry (1979). | |
Porous rocks can contain water, oil, and gas, among other things. However, if the pores are not connected to each other, these fluids will be unable to flow towards a well. They will remain trapped in the pore spaces. The degree to which pores are interconnected is referred to as the permeability. The higher the permeability, the faster liquids and gases can flow through a material.
Geologists are interested in porosity and permeability because these characteristics determine whether or not oil and gas production is feasible in a particular rock formation. The rate of production is directly related to how quickly oil and gas can move through permeable rocks. Because of this, there is a strong incentive to be able to predict how fluids will flow through permeable materials.
The relationship between permeability, porosity, and the rate at which fluids flow underground is what Darcy’s Law is all about.
Let’s take a look at how reservoir engineers, geologists, and drillers use Darcy’s Law to plan and carry out oil and gas production.
The real world is not quite a simple as Darcy’s experiment. Obviously, liquids moving underground do not flow through confined pipes. Instead, they flow through a three-dimensional mass of permeable rock.
In many rocks, the permeability varies directionally as well as between layers and types. Often, horizontal permeability is greater than vertical permeability because of the way the rocks are layered.
In the oil and gas industry, complex computer models use a 3D version of Darcy’s Law to predict the rate and direction of flow. For our purposes, a few simple rules about the flow of liquids in permeable materials will go a long way.
- Liquids always flow from regions of high pressure to regions of low pressure.
- Liquids always flow along the direction of most rapid pressure change if the permeability is high enough.
- A higher permeability rock will allow liquids to pass through more rapidly.
- The higher the viscosity of a fluid, the more slowly it will flow.
These simple rules won’t give you numerical results, but allow for an intuitive understanding of what is going on in a particular oilfield or producing well.
Oilfield Units
The units used in the oil field are often different than those used by scientists and engineers in other fields. Sometimes, the difference in units is due to differing conventions. In other cases, units are defined so that they are more convenient for describing the extreme conditions beneath the Earth’s surface. One such unit is the “Darcy.”
- The Darcy
-
A Darcy is a unit of permeability. In general, permeability has units of meters squared. One Darcy represents a permeability of approximately 10-12 m2. In porous rock units, such low permeabilities are common. The use of the Darcy is convenient because it allows us to write common permeability values without using scientific notation. A Milledarcy is equal to .001 Darcies.
Example: the Movement of Groundwater
As you know, oil and gas deposits are usually associated with brine – groundwater containing salt and other dissolved minerals. In many cases, the movement of groundwater and the migration of oil and gas are closely related.
Before we can apply Darcy’s Law to the movement of groundwater, we need to talk about a concept called hydraulic head (although the prefix “hydro” term refers to water, the same concept applies to other liquids like oils).
Hydraulic head is a way to describe the gravitational potential energy of a liquid. The higher the surface of a liquid is above a base level, the more energy it can release by flowing downhill. Areas with a high hydraulic head experience higher pressures at a given depth than areas with lower hydraulic head. Applying Darcy’s law, we can see that liquids will flow from regions of high hydraulic head to regions of low hydraulic head.
Hydraulic head can be measured by drilling a hole into an aquifer and letting it fill up with water from the surrounding rocks. The height of the water above a consistent datum is the hydraulic head.
In unconfined aquifers, hydraulic head is the same as the height of the water table at any given point. However, in confined reservoirs and aquifers, pressure exerted by water uphill of a given point cannot escape due to the impermeable layer bounding the top of the aquifer. When a borehole enters a confined aquifer, water will rise through the hole in the impermeable layer until it has reached the height defined by its hydraulic head. If the level of the hydraulic head is higher than the land surface, water emerges at the surface from an artesian spring.
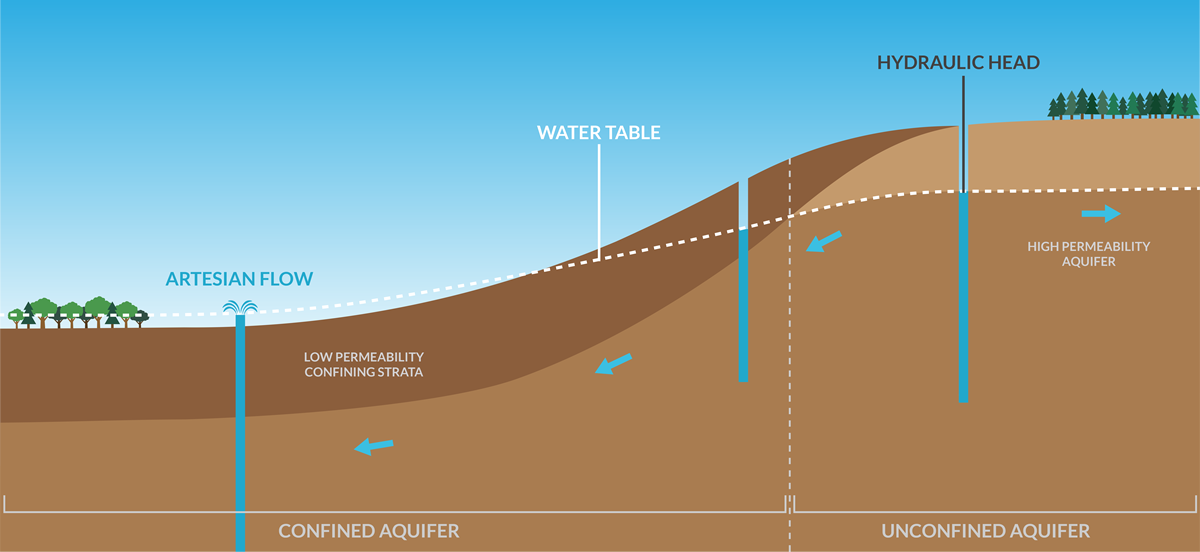
When the points representing the hydraulic head at multiple locations are connected, the resulting surface is called the potentiometric surface. The potentiometric surface represents the potential energy of the water at a given point. It is not a physical surface like the water table.
The potentiometric surface can be represented using contour lines, which describe the height of the surface above or below a chosen datum level.
In an unconfined aquifer, the potentiometric surface closely matches the shape of the water table. In a confined aquifer or reservoir, the surface can be more complex because pressure can be transmitted from distant locations, as happens at an artesian spring.
The best way to think of the potentiometric surface is as a series of hills and valleys. Liquids flow in the direction of the greatest slope of the potentiometric surface, just like rain flows down the steepest slope. This slope is called the hydraulic gradient.
The hydraulic gradient represents change in pressure over a given distance. It is the equivalent of the term from Darcy’s Law:
$$ \frac {P_b-P_a}{L} $$
We can rewrite the equation to reflect this fact:
$$ R = \frac {k}{μ}\times \frac {P_b-P_a}{L} \Rightarrow \frac {k}{μ} \times \text{hydraulic gradient}$$
As the hydraulic gradient increases, the flow rate increases.
Measuring Porosity and Permeability in the Reservoir
In order to apply Darcy’s Law in the oil field, we need to know the characteristics of the local rocks. Most boreholes intersect many different rock layers, each with a characteristic porosity and permeability. Therefore, reservoir engineers need many sets of porosity and permeability measurements to make accurate predictions. Since an understanding of fluid flow is critical for the effective management of a well, drillers and reservoir engineers invest time and money in the characterization of the rocks being drilled through.
During drilling, rock fragments are brought to the surface by the drilling mud. Geologists can make very thin slices of these fragments and study them under the microscope. This allows them to estimate porosity visually.
Low Porosity

High Porosity

Another way to measure porosity is to lower a machine that measures density down the borehole. This method gives a continuous estimate of porosity all the way to the bottom of the well and allows reservoir engineers to make more detailed models.
In contrast to porosity, which can be measured in the field, permeability needs to be measured in the lab. During drilling, a special bit is used to extract intact core samples that are several inches long. To determine the porosity, geologists dry the samples and use a special machine called a permeameter to pass compressed gas through them. The rate at which the gas passes through can be used to determine the permeability.
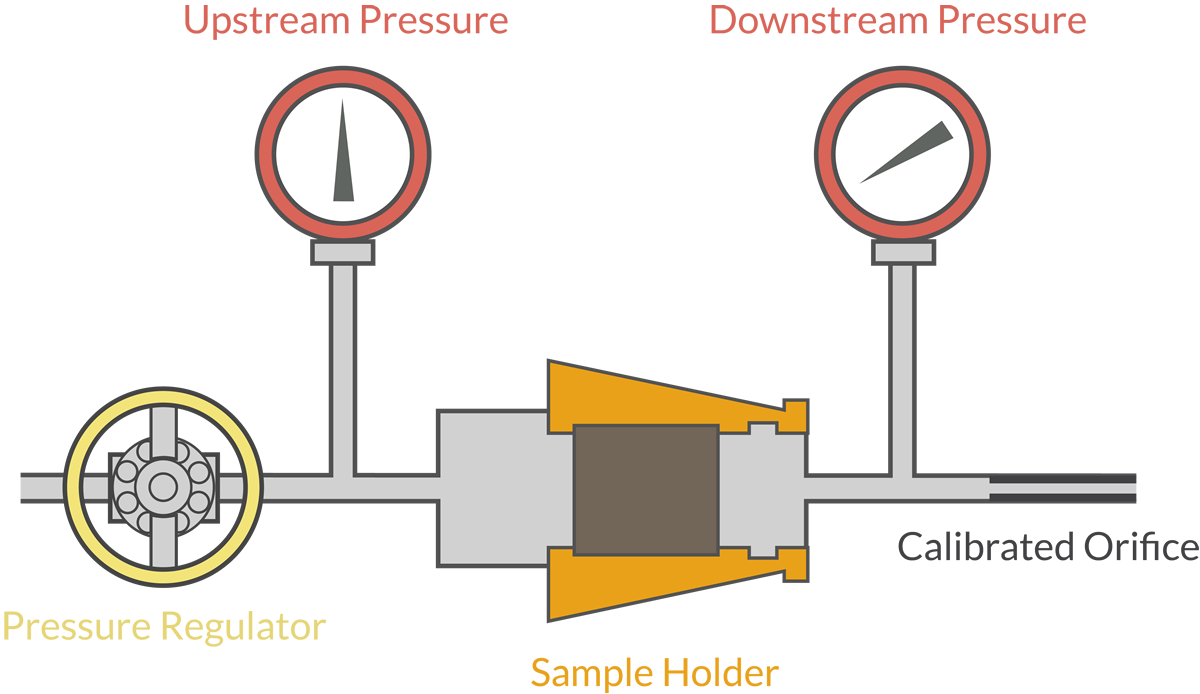
The permeameter works very similarly to Henry Darcy’s original experiment. It’s still about forcing fluids through a column of some permeable substance. It’s just a bit more technologically advanced.
All of this experimentation gets us a nice picture of the subsurface conditions of our target formation. Once we understand the local porosity and permeability characteristics of a field in three dimensions, we start getting into field drive mechanics, and that is a topic we can save for later.